.ipynb .pdf

repositorio

Binder

Contenido

Ejercicio análisi exploratorio parte 2

Utilizando los mimos datos sobre automoviles, responda a las siguientes preguntas

1. ¿Existe alguna relacion entre el territorio y los caballos de potencia?

2. ¿Cuál es la correlación entre los caballos de potencia y las millas por galón?

3. ¿Si existiese una relación, ambas variables se mueven en la misma dirección?

4. Compruebe la dirección de la relación con una visualización.

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

autos = pd.read_csv(os.path.join("./csv/", "datos_automoviles.csv"))
autos.head()

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <module>
      2 import pandas as pd
      3 import numpy as np
----> 4 import matplotlib.pyplot as plt
      5 import seaborn as sns
      7 autos = pd.read_csv(os.path.join("./csv/", "datos_automoviles.csv"))

ModuleNotFoundError: No module named 'matplotlib'

1. ¿Existe alguna relacion entre el territorio y los caballos de potencia?

territorio es una variable categórica, por tanto, no es posible calcular la correlación con caballos_potencia. Pero, como territorio solo puede tomar 3 valores (Europe, Japan, USA), convertir cada valor en un número y crear una nueva columna que tenga el territorio almacenado como un número. Así, sí es posible calcular la correlación.

# Se crea la nueva columna
def territorio_a_num(territorio):
    serie_paises = ['Europe', 'USA', 'Japan']
    if territorio == serie_paises[0]:
        return 1
    elif territorio == serie_paises[1]:
        return 2
    elif territorio == serie_paises[2]:
        return 3
    
autos['territorio_num'] = autos['territorio'].map(territorio_a_num)

# La correlación entre las variables
autos.corr()['territorio_num']['caballos_potencia']

-0.030029215705601877

2. ¿Cuál es la correlación entre los caballos de potencia y las millas por galón?

autos_corr = autos.corr()
autos_corr

	cilindros	peso	anio	aceleracion	mpg	caballos_potencia	desplazamiento	territorio_num
cilindros	1.000000	0.895220	-0.360762	-0.522452	-0.775396	0.844158	0.951787	-0.027908
peso	0.895220	1.000000	-0.315389	-0.430086	-0.831741	0.866586	0.932475	-0.094713
anio	-0.360762	-0.315389	1.000000	0.301992	0.579267	-0.424419	-0.381714	0.143544
aceleracion	-0.522452	-0.430086	0.301992	1.000000	0.420289	-0.697124	-0.557984	-0.062585
mpg	-0.775396	-0.831741	0.579267	0.420289	1.000000	-0.778427	-0.804203	0.127164
caballos_potencia	0.844158	0.866586	-0.424419	-0.697124	-0.778427	1.000000	0.898326	-0.030029
desplazamiento	0.951787	0.932475	-0.381714	-0.557984	-0.804203	0.898326	1.000000	-0.040180
territorio_num	-0.027908	-0.094713	0.143544	-0.062585	0.127164	-0.030029	-0.040180	1.000000

autos_corr['caballos_potencia']['mpg']

-0.7784267838977761

3. ¿Si existiese una relación, ambas variables se mueven en la misma dirección?

Como se puede apreciar, la covarianza es negativa, lo cual indica que las variables se mueven en direcciones contrarias.

autos.cov()['mpg']['caballos_potencia']

-233.85792577900716

4. Compruebe la dirección de la relación con una visualización

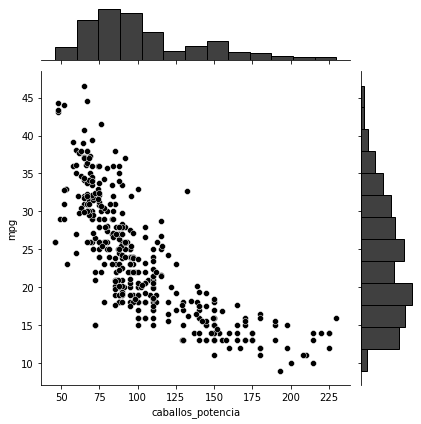
Las gráficas de regresión, se observa que la pendiente de la curva es negativa, lo cual indica que las variables son inversamente proporcionales, lo cual significa que las variables se mueven en direcciones contrarias.

# Graficar utilizando seaborn
sns.jointplot(x='caballos_potencia', y='mpg', data=autos, color='#000000')

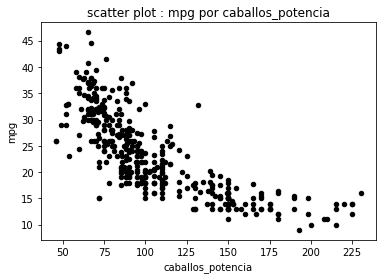
# Graficar utilizando pandas
autos.plot.scatter(x='caballos_potencia', y='mpg', color='#000000', title='scatter plot : mpg por caballos_potencia')

<AxesSubplot:title={'center':'scatter plot : mpg por caballos_potencia'}, xlabel='caballos_potencia', ylabel='mpg'>

anterior

Ejercicio análisi exploratorio parte 1

siguiente

Data Reshaping