Ejercicio análisi exploratorio parte 1
Contenido
Ejercicio análisi exploratorio parte 1¶
Utilizando los datos sobre automoviles extraídos en un archivo csv via webscraping (están almacenados en un archivo csv en la misma ruta que este notebook), responda a las siguientes preguntas:
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
automoviles = pd.read_csv('./csv/datos_automoviles.csv')
automoviles.head()
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <module>
2 import pandas as pd
3 import numpy as np
----> 4 import matplotlib.pyplot as plt
5 import seaborn as sns
7 automoviles = pd.read_csv('./csv/datos_automoviles.csv')
ModuleNotFoundError: No module named 'matplotlib'
1. La asimetría de la variable caballos_potencia es negativa?¶
print('Asimetría de caballos_potencia')
automoviles['caballos_potencia'].skew()
Asimetría de caballos_potencia
1.034079427703104
2. Entre las variables: caballos_potencia, desplazamiento, mpg y aceleracion, ¿cuáles tienen valores atípicos en ambos extremos?¶
Para saber cúales variables tiene valores atípicos, se puede utilizar gráficos o métido el analítico. En este caso, se utilizarán gráficas de dos tipos:
Una será una gráfica de distribución donde se dibujarán líneas verticales a la altura de ambos valores atípicos.
La otra, un gráfico de caja el cual nos señala mediante un círculo si existen o no valores atípicos
Cabe resaltar que la primera manera no indica de manera precisa la existencia de valores atípicos, pero se lo muestra por propósitos ilustrativos. En cambio, el gráfico de caja si indica con exactidud si existen o no valores atípicos.
def graficar_distribucion_con_valores_atipicos(columna):
q1 = automoviles.describe()[columna]['25%']
q3 = automoviles.describe()[columna]['75%']
iqr = q3 - q1
limite_derecho = q3 + 1.5 * iqr
limite_izquierdo = q1 - 1.5 * iqr
sns.kdeplot(automoviles[columna], shade=True)
plt.axvline( limite_derecho, color='b')
plt.axvline( limite_izquierdo, color='b')
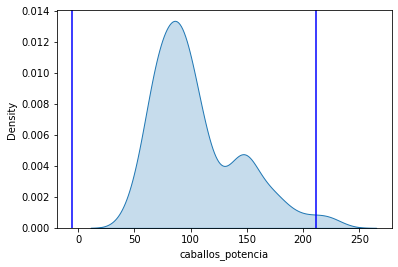
2.1 Valores atípicos caballos_potencia¶
graficar_distribucion_con_valores_atipicos('caballos_potencia')
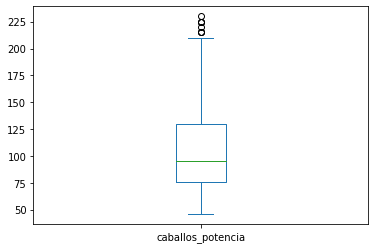
automoviles['caballos_potencia'].plot.box()
<AxesSubplot:>
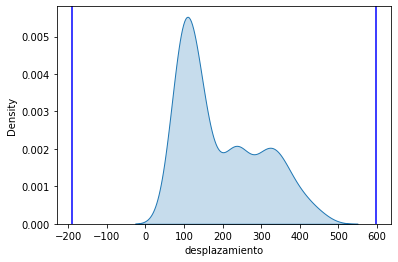
2.2 Valores atípicos desplazamiento¶
graficar_distribucion_con_valores_atipicos('desplazamiento')
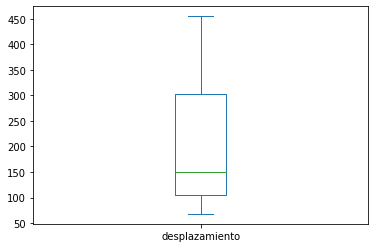
automoviles['desplazamiento'].plot.box()
<AxesSubplot:>
2.3 Valores atípicos mpg¶
graficar_distribucion_con_valores_atipicos('mpg')
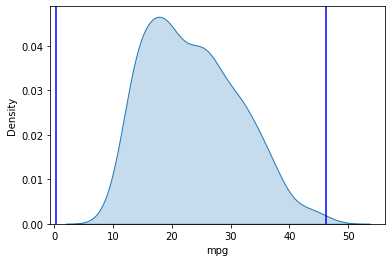
automoviles['mpg'].plot.box()
<AxesSubplot:>
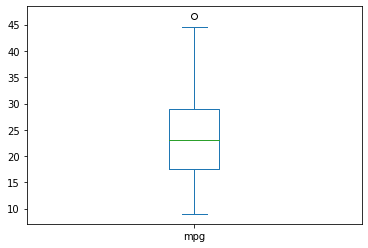
2.4 Valores atípicos aceleracion¶
graficar_distribucion_con_valores_atipicos('aceleracion')
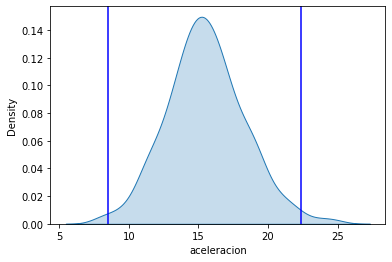
automoviles['aceleracion'].plot.box()
<AxesSubplot:>
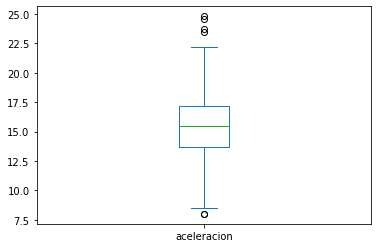
Respuesta pregunta 2: la aceleración es la única variable que tiene valores atípicos en ambos extremos¶
3. Entre las variables: caballos_potencia, desplazamiento, mpg y aceleracion, ¿cuáles no tienen valores atípicos?¶
Sobre la base de los gráficos hechos en el anterior inciso, desplazamiento es la variable que no tiene valores atípicos
4. Entre las variables: caballos_potencia, desplazamiento, mpg y aceleracion, ¿cuáles son las variables con mayor y menor asimetría?¶
print('caballos_potencia: ', automoviles['caballos_potencia'].skew())
print('desplazamiento: ', automoviles['desplazamiento'].skew())
print('mpg: ', automoviles['mpg'].skew())
print('aceleracion:', automoviles['aceleracion'].skew())
caballos_potencia: 1.034079427703104
desplazamiento: 0.6941299865999901
mpg: 0.45706634399491936
aceleracion: 0.23022375946556034
5. Entre las variables: caballos_potencia, desplazamiento, mpg y aceleracion, muestre los valores atípicos de aquellas variables que los tengan en ambos extremos¶
Como se pudo observar en el inciso 2 la variable aceleracion es la única que tiene valores atípicos en ambos extremos.
q1 = automoviles.describe()['aceleracion']['25%']
q3 = automoviles.describe()['aceleracion']['75%']
iqr = q3 - q1
limite_derecho = q3 + 1.5 * iqr
limite_izquierdo = q1 - 1.5 * iqr
Valores atípicos menores o iguales al límite inferior:
automoviles.loc[automoviles['aceleracion'] <= limite_izquierdo]
| nombre | cilindros | peso | anio | territorio | aceleracion | mpg | caballos_potencia | desplazamiento | |
|---|---|---|---|---|---|---|---|---|---|
| 16 | Plymouth 'Cuda 340 | 8 | 3609 | 1970 | USA | 8.0 | 14.0 | 160.0 | 340.0 |
| 17 | Ford Mustang Boss 302 | 8 | 3353 | 1970 | USA | 8.0 | NaN | 140.0 | 302.0 |
Valores atípicos mayores o iguales al límite superior:
automoviles.loc[automoviles['aceleracion'] >= limite_derecho]
| nombre | cilindros | peso | anio | territorio | aceleracion | mpg | caballos_potencia | desplazamiento | |
|---|---|---|---|---|---|---|---|---|---|
| 66 | Volkswagen Type 3 | 4 | 2254 | 1972 | Europe | 23.5 | 23.0 | 54.0 | 97.0 |
| 306 | Peugeot 504 | 4 | 3190 | 1979 | Europe | 24.8 | 27.2 | 71.0 | 141.0 |
| 333 | Vw Dasher (Diesel) | 4 | 2335 | 1980 | Europe | 23.7 | 43.4 | 48.0 | 90.0 |
| 402 | Vw Pickup | 4 | 2130 | 1982 | Europe | 24.6 | 44.0 | 52.0 | 97.0 |
Hay alguna relacion entre el territorio y los caballos de potencia?
Hay correlación entre los caballos de potencia y las millas por galón?
Si existe es un relación, ambas variables se mueven en la misma dirección?
Compruebe la dirección de la relación con una visualización.
def territorio_escrito_a_num(territorio):
return territorio.map({ 'Europe': 1, 'USA': 2, 'Japan': 3 })
automoviles['territorio_num'] = territorio_escrito_a_num(automoviles['territorio'])
automoviles
| nombre | cilindros | peso | anio | territorio | aceleracion | mpg | caballos_potencia | desplazamiento | territorio_num | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Chevrolet Chevelle Malibu | 8 | 3504 | 1970 | USA | 12.0 | 18.0 | 130.0 | 307.0 | 2 |
| 1 | Buick Skylark 320 | 8 | 3693 | 1970 | USA | 11.5 | 15.0 | 165.0 | 350.0 | 2 |
| 2 | Plymouth Satellite | 8 | 3436 | 1970 | USA | 11.0 | 18.0 | 150.0 | 318.0 | 2 |
| 3 | Amc Rebel Sst | 8 | 3433 | 1970 | USA | 12.0 | 16.0 | 150.0 | 304.0 | 2 |
| 4 | Ford Torino | 8 | 3449 | 1970 | USA | 10.5 | 17.0 | 140.0 | 302.0 | 2 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 401 | Ford Mustang Gl | 4 | 2790 | 1982 | USA | 15.6 | 27.0 | 86.0 | 140.0 | 2 |
| 402 | Vw Pickup | 4 | 2130 | 1982 | Europe | 24.6 | 44.0 | 52.0 | 97.0 | 1 |
| 403 | Dodge Rampage | 4 | 2295 | 1982 | USA | 11.6 | 32.0 | 84.0 | 135.0 | 2 |
| 404 | Ford Ranger | 4 | 2625 | 1982 | USA | 18.6 | 28.0 | 79.0 | 120.0 | 2 |
| 405 | Chevy S-10 | 4 | 2720 | 1982 | USA | 19.4 | 31.0 | 82.0 | 119.0 | 2 |
406 rows × 10 columns
automoviles.corr()
| cilindros | peso | anio | aceleracion | mpg | caballos_potencia | desplazamiento | territorio_num | |
|---|---|---|---|---|---|---|---|---|
| cilindros | 1.000000 | 0.895220 | -0.360762 | -0.522452 | -0.775396 | 0.844158 | 0.951787 | -0.027908 |
| peso | 0.895220 | 1.000000 | -0.315389 | -0.430086 | -0.831741 | 0.866586 | 0.932475 | -0.094713 |
| anio | -0.360762 | -0.315389 | 1.000000 | 0.301992 | 0.579267 | -0.424419 | -0.381714 | 0.143544 |
| aceleracion | -0.522452 | -0.430086 | 0.301992 | 1.000000 | 0.420289 | -0.697124 | -0.557984 | -0.062585 |
| mpg | -0.775396 | -0.831741 | 0.579267 | 0.420289 | 1.000000 | -0.778427 | -0.804203 | 0.127164 |
| caballos_potencia | 0.844158 | 0.866586 | -0.424419 | -0.697124 | -0.778427 | 1.000000 | 0.898326 | -0.030029 |
| desplazamiento | 0.951787 | 0.932475 | -0.381714 | -0.557984 | -0.804203 | 0.898326 | 1.000000 | -0.040180 |
| territorio_num | -0.027908 | -0.094713 | 0.143544 | -0.062585 | 0.127164 | -0.030029 | -0.040180 | 1.000000 |
Los caballos de potención tienen una relación con las millas por galón, debido el valor de correlación es 0.77 y es próximo a -1. Lo cual indica una relación inversa.
automoviles.plot.scatter(x='caballos_potencia', y='mpg', color='c', title='scatter plot : Tip by Total bill', alpha=0.1)
<AxesSubplot:title={'center':'scatter plot : Tip by Total bill'}, xlabel='caballos_potencia', ylabel='mpg'>
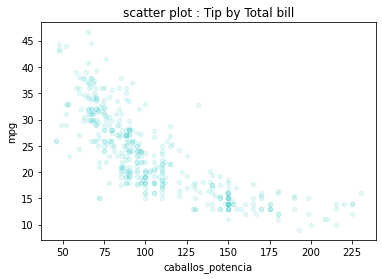
No se mueven en la misma dirección
automoviles.cov()
| cilindros | peso | anio | aceleracion | mpg | caballos_potencia | desplazamiento | territorio_num | |
|---|---|---|---|---|---|---|---|---|
| cilindros | 2.931491 | 1298.254662 | -2.315526 | -2.507662 | -10.308911 | 56.184831 | 170.982829 | -0.029265 |
| peso | 1298.254662 | 717416.332056 | -1001.421626 | -1021.220272 | -5505.211745 | 28538.206404 | 82868.813665 | -49.132056 |
| anio | -2.315526 | -1001.421626 | 14.053032 | 3.173656 | 16.741163 | -61.462080 | -150.138405 | 0.329563 |
| aceleracion | -2.507662 | -1021.220272 | 3.173656 | 7.858821 | 9.058930 | -75.801907 | -164.122683 | -0.107452 |
| mpg | -10.308911 | -5505.211745 | 16.741163 | 9.058930 | 61.089611 | -233.857926 | -655.402318 | 0.608486 |
| caballos_potencia | 56.184831 | 28538.206404 | -61.462080 | -75.801907 | -233.857926 | 1503.018239 | 3666.724846 | -0.713434 |
| desplazamiento | 170.982829 | 82868.813665 | -150.138405 | -164.122683 | -655.402318 | 3666.724846 | 11008.722272 | -2.581919 |
| territorio_num | -0.029265 | -49.132056 | 0.329563 | -0.107452 | 0.608486 | -0.713434 | -2.581919 | 0.375090 |
