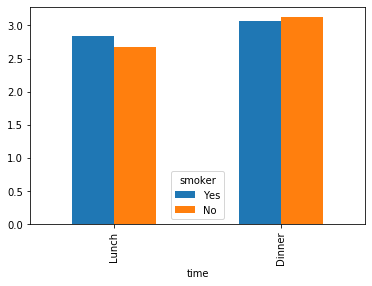.ipynb .pdf

repositorio

Binder

Contenido

Análisis exploratorio de datos multivariable

Objetivo

Identificar las correlaciones que existen en las variables para así poder formular hipótesis sobre relaciones causa-efecto.

Técnicas de análisis

1. Covarianza

2. Coeficiente de correlación

3. Visualización de la relación entre dos variables

4. Variables cualitativas

   1. Crosstabs

   2. Pivot table (Tablas de contingencia)

Carga de datos

Fuente de datos

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

tips = sns.load_dataset('tips')
tips.tail()

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <module>
      2 import pandas as pd
      3 import numpy as np
----> 4 import matplotlib.pyplot as plt
      5 import seaborn as sns
      7 tips = sns.load_dataset('tips')

ModuleNotFoundError: No module named 'matplotlib'

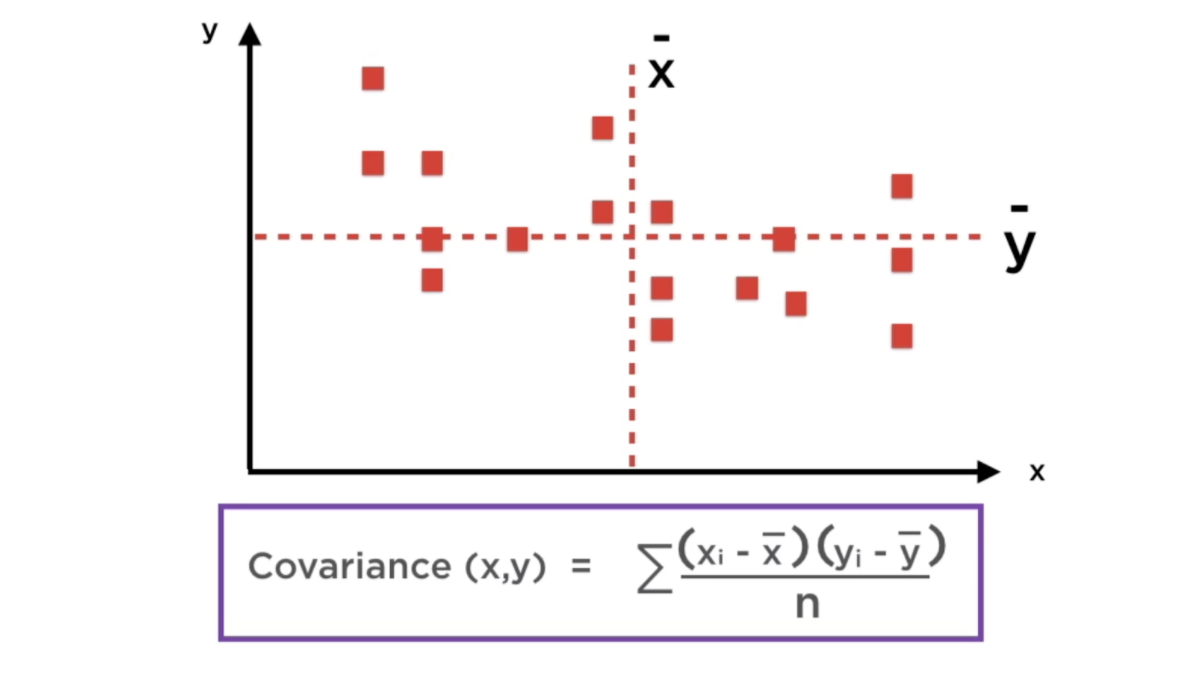
Covarianza

Mide la relación lineal entre dos variables (si incrementan o decrementan juntas). Una covarianza positiva indica que las variables se mueven en la misma dirección y un covarianza negativa que las variables cambian en direcciones opuestas. Sin embargo, no permite valorar la intensidad de la relación.

np.cov(tips['total_bill'], tips['tip'])

array([[79.25293861,  8.32350163],
       [ 8.32350163,  1.91445464]])

tips.cov()

	total_bill	tip	size
total_bill	79.252939	8.323502	5.065983
tip	8.323502	1.914455	0.643906
size	5.065983	0.643906	0.904591

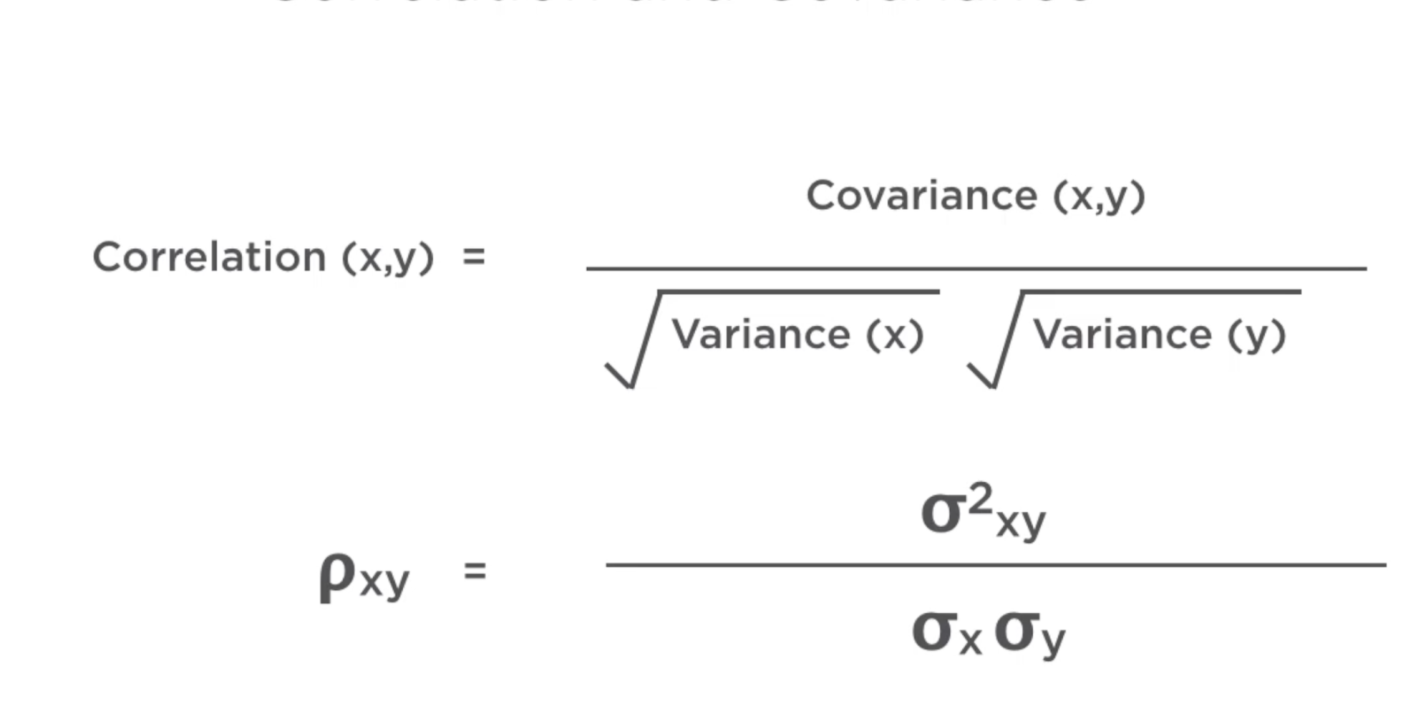
Coeficiente de correlación

Al igual que la covarianza mide la dirección pero tambien la intensidad de la relación. Es importante recordar que correlación no implica causalidad

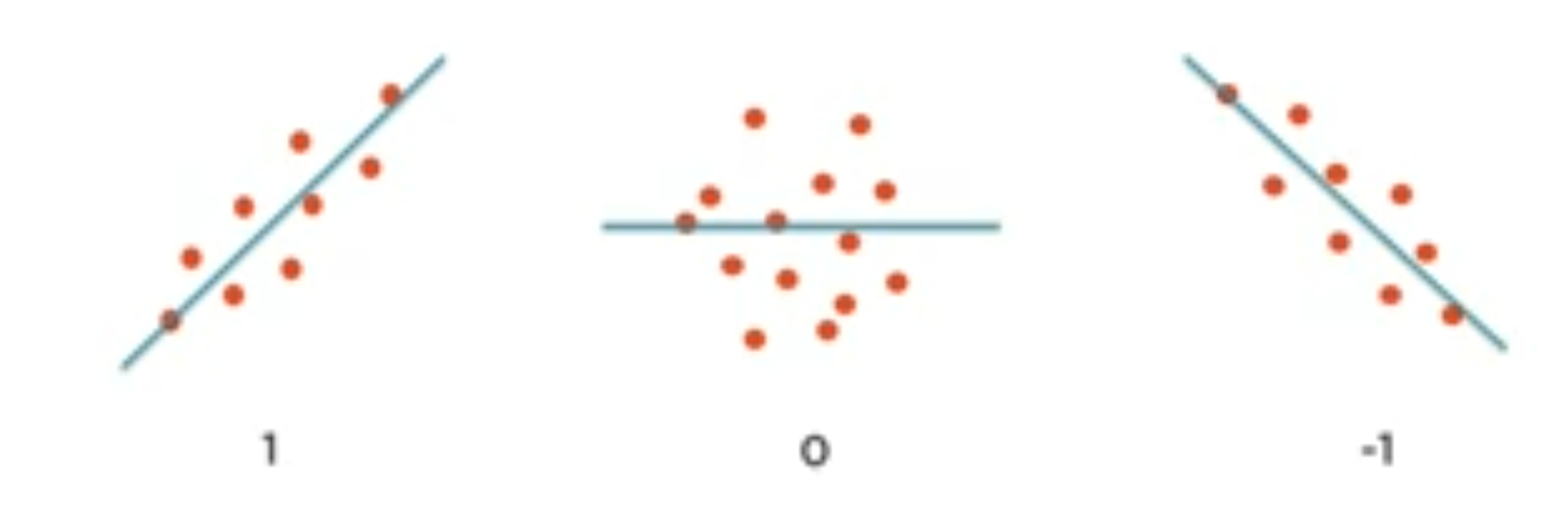
Un coeficiente de correlación igual a cero no necesarimente implica que las variables sean independientes. Dos variables independientes tendrán un coefiente de correlación de cero. Por esta razón, el cálculo del coeficiente de correlación debe ser complementado con la exploración visual de los datos..

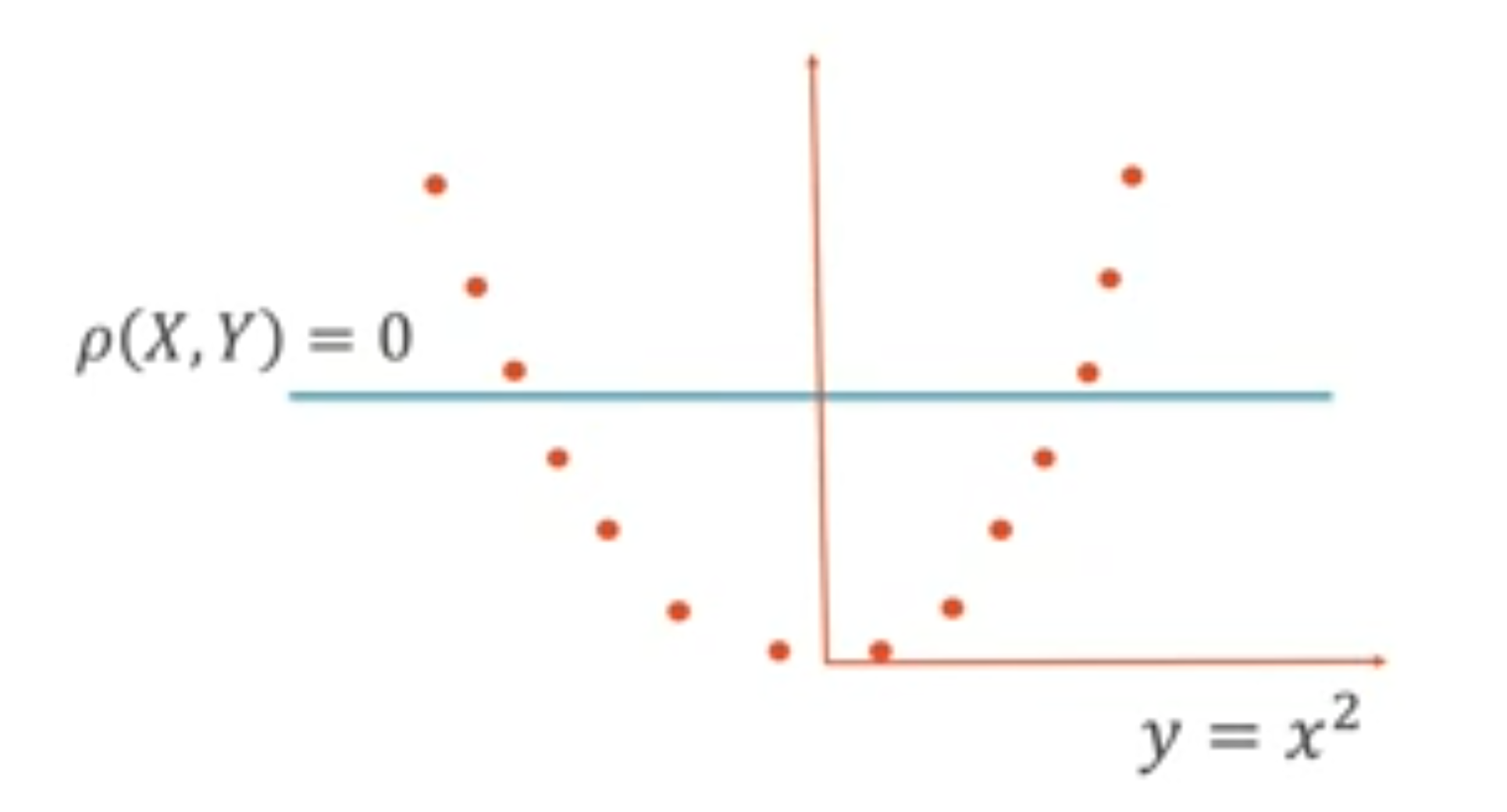
Tambien es importante recordar que el índice de correlación sólo indica relaciones lineales entre las variables. Por tanto, no indica las relaciones no lineales que pudieran existir entre las variables. Por ejemplo, en la ecuación y=x^2, las variables tendrán una correlación de 0 a pesar de estar claramente relacionadas.

np.corrcoef(tips['total_bill'], tips['tip'])

array([[1.        , 0.67573411],
       [0.67573411, 1.        ]])

tips.corr()

	total_bill	tip	size
total_bill	1.000000	0.675734	0.598315
tip	0.675734	1.000000	0.489299
size	0.598315	0.489299	1.000000

Visualización de la relación entre dos variables

Seaborn

matplotlib

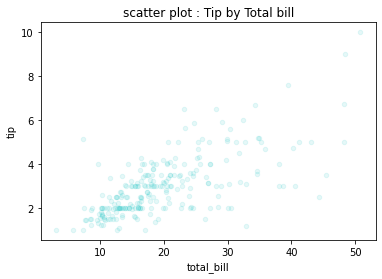
tips.plot.scatter(x='total_bill', y='tip', color='c', title='scatter plot : Tip by Total bill', alpha=0.1)

<AxesSubplot:title={'center':'scatter plot : Tip by Total bill'}, xlabel='total_bill', ylabel='tip'>

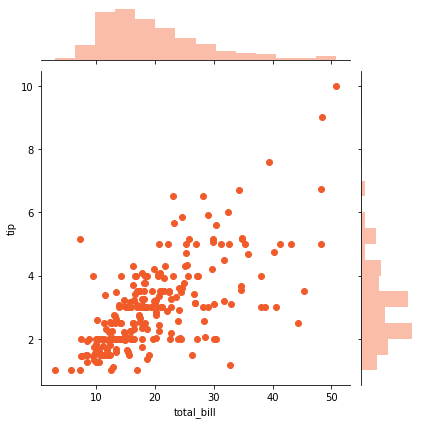
sns.jointplot(x='total_bill', y='tip', data=tips, color='#F15B2A')

<seaborn.axisgrid.JointGrid at 0x7f151e4395d0>

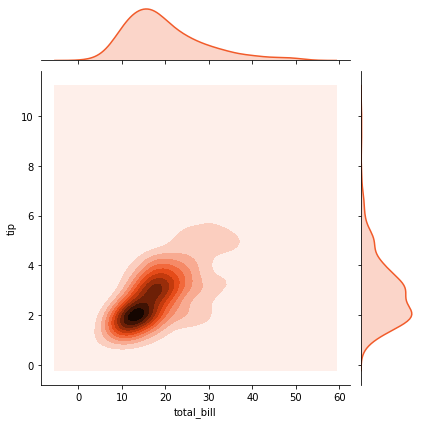
sns.jointplot(x='total_bill', y='tip', data=tips, color='#F15B2A', kind='kde')

<seaborn.axisgrid.JointGrid at 0x7f151e8c3350>

Variables cualitativas

Crosstabs

tips.head()

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2
1	10.34	1.66	Male	No	Sun	Dinner	3
2	21.01	3.50	Male	No	Sun	Dinner	3
3	23.68	3.31	Male	No	Sun	Dinner	2
4	24.59	3.61	Female	No	Sun	Dinner	4

#Conteos de la combinacion de variables nominales
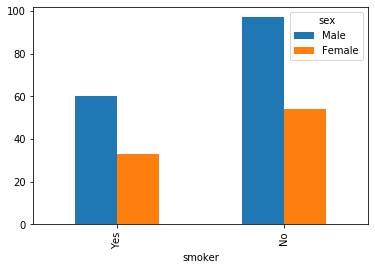
pd.crosstab(tips["smoker"], tips["sex"])

sex	Male	Female
smoker
Yes	60	33
No	97	54

pd.crosstab(tips["smoker"], tips["sex"]).plot(kind='bar')

<matplotlib.axes._subplots.AxesSubplot at 0x7f151e27dd50>

Pivot (tablas de contingencia)

Es una extensión del crosstab que permite analizar dos variables categóricas y una numérica.

tips.pivot_table(index='time',columns = 'smoker',values='tip', aggfunc='mean')

smoker	Yes	No
time
Lunch	2.834348	2.673778
Dinner	3.066000	3.126887

tips.groupby(['time','smoker'])['tip'].mean()
#type(tips.groupby(['time','smoker'])['tip'].mean())

time    smoker
Lunch   Yes       2.834348
        No        2.673778
Dinner  Yes       3.066000
        No        3.126887
Name: tip, dtype: float64

tips.groupby(['time','smoker'])['tip'].mean().unstack()

smoker	Yes	No
time
Lunch	2.834348	2.673778
Dinner	3.066000	3.126887

tips.groupby(['time','smoker'])['tip'].mean().unstack().plot.bar()

<matplotlib.axes._subplots.AxesSubplot at 0x7f151e6bda90>

anterior

Análisis unidimensional

siguiente

Ejercicio análisi exploratorio parte 1