Ejercicio misceláneo: Feature Selection, Modelos predictivos
Contenido
Ejercicio misceláneo: Feature Selection, Modelos predictivos¶
1. En un filtro antispam ¿prefeririría que sea más alta la presición o la exhaustividad? Justifique su respuesta.¶
Asuma que el filtro elimina cualquier mensaje que detecte como spam.
En este caso, es más importante tener una alta precisión. Porque una alta precisión significa que el número de falsos positivos es reducido. Es mucho peor tener un falso positivo que un falso negativo. Porque, digamos, si tengo un correo muy importante sobre trabajo y se lo marca como spam, es catastrófico. En cambio, si me llega un correo spam a mi bandeja de entrada, no es algo tan molesto.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score, f1_score
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Input In [1], in <module>
1 import pandas as pd
2 import numpy as np
----> 3 import matplotlib.pyplot as plt
4 import os
6 from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score, f1_score
ModuleNotFoundError: No module named 'matplotlib'
diabetes_df = pd.read_csv(os.path.join("datasets","diabetes.csv"))
diabetes_df.head()
| Pregnancies | Glucose | BP | Skin Thickness | Insulin | Mass | Pedigree | Age | class | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 | 0 | 33.6 | 0.627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26.6 | 0.351 | 31 | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23.3 | 0.672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28.1 | 0.167 | 21 | 0 |
| 4 | 0 | 137 | 40 | 35 | 168 | 43.1 | 2.288 | 33 | 1 |
VARIABLES_INDEPENDIENTES = list(diabetes_df.columns[:-1])
VARIABLES_INDEPENDIENTES
['Pregnancies',
'Glucose',
'BP',
'Skin Thickness',
'Insulin',
'Mass',
'Pedigree',
'Age']
2 Feature selection¶
En el siguiente problema de clasificación. Determine el porcentaje adecuado de variables aplicando la Información mutua. El valor a partir de cual un incremento en el mismo no incrementa significativamente el desempeño del clasificador (2% o menos)
from sklearn.feature_selection import mutual_info_classif, SelectPercentile
def seleccionar_variables(X, Y, porcentaje):
X_as_float = X.astype(np.float64)
select_features = SelectPercentile(mutual_info_classif, porcentaje)
X_new = select_features.fit_transform(X_as_float, Y)
return X_new
def datos_performance(performance_clasificador):
exactitud = [performance_clasificador[key]['exactitud'] for key in performance_clasificador]
nro_variables = list(range (1, 100, 10))
return pd.DataFrame(data={'exactitud' : exactitud}, index = nro_variables)
from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score, f1_score
def evaluar_clasificador(variable_dependiente,
variables_independientes,
data_frame,
porcentaje):
Y = data_frame[variable_dependiente]
X = seleccionar_variables(data_frame[variables_independientes], Y, porcentaje)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
clasificador = LogisticRegression(solver = 'liblinear')
clasificador.fit(X_train, Y_train)
return {'exactitud': accuracy_score(Y_test, clasificador.predict(X_test)),
'precision' : precision_score(Y_test, clasificador.predict(X_test)),
'exhaustividad' : recall_score(Y_test, clasificador.predict(X_test))}
performance_clasificador = {}
for i in range (1, 100, 10):
performance_clasificador['mutual_info_classif percentile - ' + str(i)] = evaluar_clasificador('class',
VARIABLES_INDEPENDIENTES,
diabetes_df,
i)
df = datos_performance(performance_clasificador)
df.head(10)
| exactitud | |
|---|---|
| 1 | 0.772727 |
| 11 | 0.779221 |
| 21 | 0.746753 |
| 31 | 0.766234 |
| 41 | 0.720779 |
| 51 | 0.740260 |
| 61 | 0.746753 |
| 71 | 0.792208 |
| 81 | 0.766234 |
| 91 | 0.746753 |
df.plot.line(rot=0)
<matplotlib.axes._subplots.AxesSubplot at 0x7f03bd0ddf10>
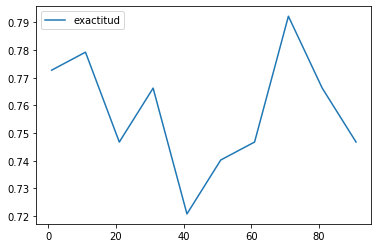
El porcentaje adecuado de variables es el 71%. Con ese número de variables se tiene la mayor exactitud. Además, si se incrementa el valor (81%), se observa que la exactitud reduce. Y este valor tiene una diferencia de más del 2 por ciento que el valor inmediatamente anterior (61%).
