.ipynb .pdf

repositorio

Binder

Ejercicio Regresión Logística

Crear un clasificador basado en el algoritmo de regresión logistica para predecir si el valor de la vivienda supera la media

entrada: housing.csv

Procedimiento:

• Cargar los datos los datos a un DataFrame y explorar brevemente

• Eliminar las observaciones que tengan algun dato faltante

• Eliminar las observaciones con el valor atípico (max) para la variable “median_house_value”

• Aplicar one hot encoding a la variable “ocean_proximity”

• Crear una nueva variable boolean “above_median”

• Aplicar los pasos train-test-split para poder entrenar y evaluar el clasificador

Cuáles los valores para accuracy, matriz de confusion, precision, recall y f1 del clasificador?

import os
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_boston

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <module>
      2 import numpy as np
      3 import pandas as pd
----> 4 from sklearn.model_selection import train_test_split
      5 from sklearn.linear_model import LogisticRegression
      6 from sklearn.datasets import load_boston

ModuleNotFoundError: No module named 'sklearn'

# Cargar los datos los datos a un DataFrame y explorar brevemente
housing_csv_df = pd.read_csv(os.path.join("", "housing.csv"))
housing_csv_df.head()

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	expected_house_value	ocean_proximity
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	NEAR BAY
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	NEAR BAY
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	NEAR BAY
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	NEAR BAY
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	NEAR BAY

# Eliminar las observaciones que tengan algun dato faltante
housing_csv_df.loc[housing_csv_df['total_bedrooms'].isnull()]
housing_sin_valores_na = housing_csv_df.dropna(how='any')

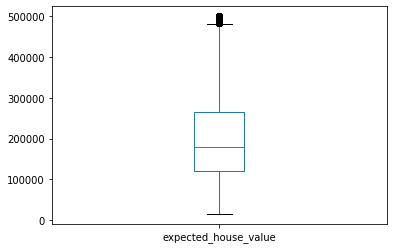
# Eliminar las observaciones con el valor atípico (max) para la variable 'median_house_value'
housing_sin_valores_na['expected_house_value'].plot.box()

<matplotlib.axes._subplots.AxesSubplot at 0x7f88b82f6490>

q1 = housing_sin_valores_na['expected_house_value'].quantile(.25)
q3 = housing_sin_valores_na['expected_house_value'].quantile(.75)
iqr = q3 - q1
indices_val_atipicos_max = housing_sin_valores_na.loc[housing_sin_valores_na['expected_house_value'] > q3 + 1.5*iqr].index
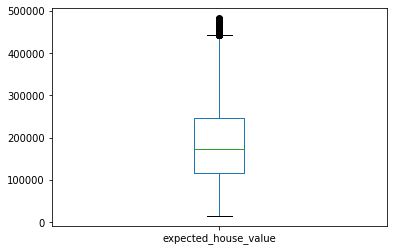
housing_sin_val_atip = housing_sin_valores_na.drop(indices_val_atipicos_max, axis=0)
housing_sin_val_atip['expected_house_value'].plot.box()

<matplotlib.axes._subplots.AxesSubplot at 0x7f88b7a94150>

# Aplicar one hot encoding a la variable 'ocean_proximity'
housing_procesado = pd.get_dummies(housing_sin_val_atip, columns=['ocean_proximity'])
housing_procesado

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	expected_house_value	ocean_proximity_<1H OCEAN	ocean_proximity_INLAND	ocean_proximity_ISLAND	ocean_proximity_NEAR BAY	ocean_proximity_NEAR OCEAN
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	0	0	0	1	0
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	0	0	0	1	0
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	0	0	0	1	0
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	0	0	0	1	0
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	0	0	0	1	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0	0	1	0	0	0
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0	0	1	0	0	0
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0	0	1	0	0	0
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0	0	1	0	0	0
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0	0	1	0	0	0

19369 rows × 14 columns

# Crear una nueva variable boolean 'above_median'
media_expexted_house_value = housing_procesado['expected_house_value'].mean()
housing_procesado['above_median'] = housing_procesado['expected_house_value'] > media_expexted_house_value
housing_procesado

	longitude	latitude	housing_median_age	total_rooms	total_bedrooms	population	households	median_income	expected_house_value	ocean_proximity_<1H OCEAN	ocean_proximity_INLAND	ocean_proximity_ISLAND	ocean_proximity_NEAR BAY	ocean_proximity_NEAR OCEAN	above_median
0	-122.23	37.88	41.0	880.0	129.0	322.0	126.0	8.3252	452600.0	0	0	0	1	0	True
1	-122.22	37.86	21.0	7099.0	1106.0	2401.0	1138.0	8.3014	358500.0	0	0	0	1	0	True
2	-122.24	37.85	52.0	1467.0	190.0	496.0	177.0	7.2574	352100.0	0	0	0	1	0	True
3	-122.25	37.85	52.0	1274.0	235.0	558.0	219.0	5.6431	341300.0	0	0	0	1	0	True
4	-122.25	37.85	52.0	1627.0	280.0	565.0	259.0	3.8462	342200.0	0	0	0	1	0	True
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
20635	-121.09	39.48	25.0	1665.0	374.0	845.0	330.0	1.5603	78100.0	0	1	0	0	0	False
20636	-121.21	39.49	18.0	697.0	150.0	356.0	114.0	2.5568	77100.0	0	1	0	0	0	False
20637	-121.22	39.43	17.0	2254.0	485.0	1007.0	433.0	1.7000	92300.0	0	1	0	0	0	False
20638	-121.32	39.43	18.0	1860.0	409.0	741.0	349.0	1.8672	84700.0	0	1	0	0	0	False
20639	-121.24	39.37	16.0	2785.0	616.0	1387.0	530.0	2.3886	89400.0	0	1	0	0	0	False

19369 rows × 15 columns

# Aplicar los pasos train-test-split para poder entrenar y evaluar el clasificador
X = housing_procesado.drop(columns=['expected_house_value']).to_numpy().astype('float')
y = housing_procesado['expected_house_value'].ravel()

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# Se crea al clasificador
clasificador_reg_log = LogisticRegression(random_state=0, solver='liblinear')
# Se entrena al clasificador
clasificador_reg_log.fit(X_train, y_train)

# accuracy
print('accuracy del clasificador: {0:.2f}'.format(accuracy_score(y_test, clasificador_reg_log.predict(X_test))))
# confusion matrix
print('matriz de confusión del clasificador: \n {0}'.format(confusion_matrix(y_test, clasificador_reg_log.predict(X_test))))
# precision 
print('precision del clasificador: {0:.2f}'.format(precision_score(y_test, clasificador_reg_log.predict(X_test))))
# recall 
print('recall del clasificador: {0:.2f}'.format(recall_score(y_test, clasificador_reg_log.predict(X_test))))
# f1
print('f1 del clasificador: {0:.2f}'.format(f1_score(y_test, clasificador_reg_log.predict(X_test))))

anterior

Arboles de decisión: Introducción

siguiente

Ejercicio misceláneo: Feature Selection, Modelos predictivos